Cours de physique
stueckelberg









Si les contributions fondamentales d’Ernst C. G. Stueckelberg von Breidenbach au développement de la mécanique quantique, de la théorie des champs et de la physique des particules élémentaires sont établies et bien reconnues, l’activité professorale du professeur Stückelberg fut tout aussi riche et remarquable. L’enseignement de la physique théorique a constitué une large part de sa carrière, à laquelle il attachait beaucoup de soin et d’attention : il dispensa cet enseignement à l’Université de Genève de 1935 à 1975 (avec une interruption entre 1950 et 1961) ainsi qu’à l’Université de Lausanne de 1942 à 1975. Quiconque assistait à l’un de ses cours réalisait immédiatement qu’il avait à faire à une personnalité exceptionnelle. Formé à l’école d’Arnold Sommerfeld, ses exposés étaient complets et détaillés, d’une logique impeccable, et déployés sur un tableau noir entièrement couvert de son écriture à la craie. Mais c’est surtout l’originalité des points de vue et l’approche non conventionnelle des sujets qui frappaient l’étudiant qui avait courageusement entrepris de remettre ses notes de cours à jour. Ainsi plusieurs générations de physiciens ont été marquées et inspirés de façon inoubliable par l’enseignement de ce maître à penser.
Malheureusement, à l’instar de sa production scientifique, les cours de Stueckelberg n’ont reçu à l’époque qu’une diffusion très limitée en dehors de la Suisse romande. Peu avant sa retraite, il entreprit la rédaction d’ouvrages pédagogiques, dont le premier, intitulé Thermocinétique phénoménologique galiléenne et écrit avec son collaborateur Paul Scheurer, a paru chez Birkhäuser en 1974. Ce texte est reproduit ici pratiquement sans modification (Livre I). Cette reprise se justifie d’une part par le fait que l’ouvrage est actuellement épuisé, mais surtout par l’importance que Stueckelberg attachait à la thermodynamique comme discipline fondamentale à la base des autres branches de la physique.
Ce livre est donc une étape nécessaire à la compréhension des démarches subséquentes exposées dans les livres suivants. On sait de la correspondance de Stueckelberg qu’il avait le projet de rédiger d’autres cours, projets qui n’ont pu être réalisés. Cependant, un certain nombre de ses élèves ont mis au net leurs notes qu’ils ont conservées jusqu’à présent. Marcel Perroud en particulier, qui a suivi l’enseignement de Stueckelberg dans la deuxième partie de la décennie 1960-1970, en a effectué une saisie informatique. Il a bien voulu nous fournir ses fichiers et proposer leur publication. Ce sont donc ces documents que nous présentons ici, dont le contenu est :
A l’exception du Livre I qui est, comme on l’a dit, de la main de Stueckelberg et Scheurer, les autres livres reflètent l’état des notes que Marcel Perroud a rédigées. Ces notes sont le résultat d’une stricte transcription des exposés de Stueckelberg prises sur le champ au fil des semaines, et n’ont pas subi le travail rédactionnel qui les constituerait en ouvrages complets et définitifs. Naturellement le contenu variait d’année en année, si bien qu’on ne trouve ici que l’image de cet enseignement à une période donnée. Toutefois, après une relecture de ces textes comparativement avec les notes manuscrites d’anciens étudiants, on peut dire qu’ils présentent une image fidèle et authentique des sujets couverts par Stueckelberg et de sa manière de les traiter.
C’est pourquoi, en dépit d’imperfections et d’erreurs possibles (qui ne sauraient être attribuées à Stueckelberg), nous avons pensé que leur mise en ligne avait un intérêt pédagogique et permettait de conserver un élément du patrimoine scientifique de la Suisse romande. La logique non usuelle de l’argumentation de Stueckelberg, jointe au fait que les livres II à VI ne contiennent que peu de commentaires explicatifs, en rend parfois la lecture difficile. Aussi chaque livre est assorti d’une brève introduction que d’anciens élèves ou collaborateurs de Stueckelberg ont bien voulu écrire. La lecture peut également être obscurcie par sa notation mathématique très personnelle et non standard. En effet Stueckelberg tenait à ce que chaque symbole soit entièrement qualifié (caractère tensoriel, comportement sous les lois de transformation, choix d’un référentiel, etc.) ce qui alourdit souvent l’écriture. Le lecteur aura avantage à parcourir l’annexe A du Livre I ainsi que l’index des notations extrait de l’ouvrage de Stueckelberg et Sheurer paru en 1974. Nous espérons que, ces difficultés surmontées, il appréciera la profondeur et la beauté de ces cours.
Nous remercions Marcel Perroud pour son travail de rédaction des notes et leur première saisie informatique et Yves Soulet pour leur mise en forme en vue de leur publication en ligne. Nous avons bénéficié du concours bénévole des professeurs W. Amrein, Ch. Gruber, F. Reuse, H. Ruegg et G. Wanders pour des commentaires et relecture soigneuses des textes, qu’ils soient également vivement remerciés. Enfin, le Département de physique de l’Université de Genève, l’Ecole polytechnique fédérale de Lausanne et la famille d’Ernst C. G. Stueckelberg ont apporté un appui financier sans lequel ce site n’aurait pas pu voir le jour.
Né à Bâle le 1er février 1905. Son nom complet est: Ernst Carl Gerlach Stueckelberg, Baron von Breidenbach zu Breidenstein und Melsbach. Il a reçu son titre de noblesse par sa mère, d’origine allemande. Stueckelberg a étudié la physique à l’Université de Bâle de 1923 à 1927, tout en séjournant à Munich pendant l’année académique 1924-1925. Il y a notamment suivi les cours d’Arnold Sommerfeld, l’un des maîtres de la physique théorique de la première moitié du 20e siècle. Stueckelberg obtient le titre de docteur es sciences en 1927.
A la fin de 1927 Stueckelberg se rend aux Etats-Unis pour occuper un poste de research associate au Palmer Physical Laboratory à Princeton. Il y devient assistant professor en 1930. Pendant son séjour, Stueckelberg travail sur les propriétés quantiques des molécules, un sujet de grande actualité à cette époque. Il a été très productif, contribuant notamment au développement du formalisme de Landau-Zener-Stueckelberg pour les collisions inélastiques entre atomes.
En 1932, il subit la première attaque d’une maladie mentale (psychose maniaco-dépressive) qui affligera gravement toute son existence. Estimant qu’il n’est plus en état de poursuivre une carrière académique aux Etats-Unis, il quitte Princeton, revient en Suisse et occupe un poste d’assistant à l’Université de Bâle.
A son retour des Etats-Uni, Stueckelberg abandonne définitivement la physique moléculaire pour se consacrer à la théorie des particules élémentaires. Il participe au développement de la théorie relativiste des champs quantifiés qui fournit la description des phénomènes impliquant des particules élémentaires.
Dans les années 1930 le problème principal est l’élucidation des forces nucléaires liant les constituants des noyaux.
Stueckelberg figure parmi les premiers, à côté de H. Yukawa, à avoir correctement suggéré que ces forces proviennent de l’échange de nouvelles particules, les mésons, entre les nucléons des noyaux, comme les forces électromagnétiques dues à l’échange de photons entre particules chargées.
En 1933, il est nommé privat-docent à l’Université de Zurich. Il y est en contact avec Gregor Wentzel et Wolfgang Pauli (de l’EPFZ), deux sommités de la physique théorique.
La carrière de Stueckelberg est définitivement assurée en 1934 lorsqu’il obtient un poste de professeur de physique théorique à l’Université de Genève. A partir de 1942 il enseigne également la physique théorique à l’Université de Lausanne, d’abord comme chargé de cours puis comme professeur.
Dans ces années, son intérêt se porte sur la matrice S , un objet introduit par W. Heisenberg groupant toutes les informations sur les processus résultant des interactions entre particules élémentaires. Stueckelberg a contribué à la construction perturbative de la matrice S , aux côtés de célébrités telles que R. P. Feynman, F. Dyson et J. Schwinger. Il a établi le rôle joué par un principe de causalité dans l’évolution d’un système de particules. Ce principe est un des éléments déterminants de la structure de la matrice S. La théorie de la matrice S a conduit à des prévisions spectaculaires en électrodynamique quantique. Stueckelberg est aussi l’inventeur du groupe de renormalisation, un outil important de la physique théorique.
Stueckelberg prend sa retraite en 1975 et meurt à Genève le 4 septembre 1984. Il a reçu le Prix des Sciences de la Ville de Genève en 1971 et la Médaille Max Planck de la Société allemande de physique en 1976.
Les travaux de Stueckelberg se sont toujours situés à la pointe de la recherche. Il a côtoyé, en chercheur original et indépendant, parfois en précurseur, les grands développements de la physique des particules élémentaires du milieu du 20e siècle. Il a ainsi émis l’idée en 1941 qu’un positron peut être considéré comme un électron remontant dans le temps. Cette idée a été reprise par R. P. Feynman en 1949.
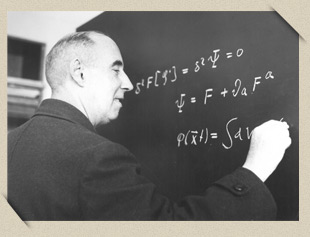
L’enseignement a occupé une bonne part de l’activité de Stueckelberg et il y a consacré beaucoup d’énergie. Il aimait donner ses cours, faire partager ainsi sa vision personnelle de l’édifice de la physique théorique.
http://www-history.mcs.st-andrews.ac.uk/Biographies/Stueckelberg.html
http://pseudopodo.wordpress.com/2006/10/03/la-increible-y-triste-historia-de-ecg-stueckelberg/
Une description de l’œuvre scientifique de Stueckelberg ainsi que la reproduction de certains de ses articles les plus importants peuvent être trouvées dans: J. Lacki, H. Ruegg et G. Wanders, E.C.G. Stückelberg, an unconventional figure of twentieth century physics, Birkhäuser, 2009.
R. Wenger, Ernst C. G. Stueckelberg von Breidenbach – Etude biographique, Université de Genève, Bibliothèque de l’Ecole de Physique, 1986.
R. P. Crease et Ch. C. Mann, « The physicist that physics forgot: Baron Stueckelberg’s brilliantly obscure career », in The Science, Juillet-août, vol. 25, 1985.
E. C. G. Stueckelberg de Breidenbach et P. B. Scheurer, Thermocinétique phénoménologique galiléenne, Birkhäuser, Bâle, 1974.
Gérard Wanders, « Stückelberg as a young man », Communications de la Société Suisse de Physique, 32, septembre 2010.
L’exposé qui suit est élémentaire, au sens ou l’entendait F. Klein lorsqu’il baptisait son traité de mathématique élémentaire. Notre but est, en effet, d’établir les lois de la physique à partir d’un système de propositions prises comme axiomes ou principes, la justification du choix de ce système se trouvant dans la vérification expérimentale des lois qu’on en déduit.
Ce but est, en fait, loin de nous être particulier. Mais notre exposé présente l’originalité de rompre avec une habitude presque traditionnelle, qui est de commencer l’étude de la physique par la mécanique rationnelle, discipline dans laquelle le point de masse s’introduit comme axiome. Au contraire, nous considérons d’emblée le continu spatio-temporel, rapporté à un référentiel {x⃗t} , non relativiste, tel qu’il se présente en fait à l’observation macroscopique d’un système substantiel pour des vitesses faibles par rapport à celle de la lumière. A cette partie de la physique, on applique le terme de phénoménologique, qui s’oppose ainsi à ceux de microscopique ou quantique employés pour designer le niveau où la discontinuité des processus joue un rôle fondamental. Par conséquent, la phénoménologie ignore le concept même de fluctuations et se doit ainsi d’éviter toute référence à la mécanique statistique.
Pour rendre notre théorie aussi générale que possible, nous considérons ce continu spatio-temporel comme formé de l’espace physique à d dimensions et d’un seul temps. Pour l’espace physique, en effet, seule la considération de l’électrodynamique et de la relativité générale est capable de fixer à 3 le nombre de ses dimensions.
D’autre part, tant qu’on se restreint à l’homogénéité de l’espace, il suffit pour celui-ci de présenter la structure d’espace affine, où la distinction entre covariance et contravariance est essentielle. Mais lorsqu’on veut prendre en considération également l’isotropie de l’espace par la définition du moment cinétique, il devient nécessaire de pouvoir changer de variance par l’introduction d’une métrique (ici constante). La structure d’espace métrique autorise du même coup l’énoncé de l’axiome de Newton, qui rend le vecteur covariant quantité de mouvement proportionnel au vecteur contravariant vitesse, avec le scalaire masse inerte comme facteur de proportionnalité. Cependant, la signature de cette métrique (définie positive, négative ou non définie) est laissée pendante jusqu’à l’application du deuxième principe, qui lui impose d’être définie. Par choix de la définition positive, l’espace est alors rendu euclidien, ce qui abolit la distinction entre covariance et contravariance.
Pour le temps, la succession des événements lui impose, au niveau phénoménologique, la structure d’un continu unidimensionnel totalement ordonné, c’est-à-dire celle de la droite réelle. Mais une structure supplémentaire vient se surimposer à la première: la flèche du temps, qui rend compte de la dissymétrie passé → futur et de l’évolution irréversible des phénomènes, caractère essentiel de la phénoménologie. Vu l’homogénéité du temps, cette évolution est soumise au déterminisme laplacien. En admettant qu’on puisse opérer la partition de l’Univers entre système (sous observation) et milieu extérieur, et que ces deux parties soient sans interaction aucune (on dit alors que le système est isolé), l’état du système à une époque quelconque détermine entièrement son état à tout autre temps, aussi bien antérieur que postérieur.
Mais précisément la flèche du temps rend ce déterminisme non réciproque. Alors qu’il est valable pour l’évolution vers le futur, il tombe en faillite quand on veut l’extrapoler à un passé assez reculé. Techniquement, cette dissymétrie provient du fait que les variables qui décrivent l’évolution de l’état du système, solutions d’équations différentielles, convergent pour le futur lointain et divergent pour le passé lointain, à cause du signe déterminé de certaines grandeurs qui interviennent dans les équations de mouvement. La plupart des traités fixent ces signes arbitrairement; notre théorie présente l’avantage de les déduire, soit absolument pour certains, soit relativement au signe de la température absolue pour d’autres.
Puisque l’irréversibilité du temps se rapporte à la non-décroissance de l’entropie, c’est bien par la thermocinétique phénoménologique que nous sommes amenés à commencer notre étude du monde physique. Si nous préférons le terme de thermocinétique à celui, traditionnel, de thermodynamique, c’est que, d’une part, les forces n’interviennent pas de façon essentielle dans notre exposé, et que, d’autre part, nous tenons ainsi à souligner notre différence d’avec les traités habituels, qui, sous le nom de thermodynamique, étudient essentiellement une thermostatique, limitée à la seule discussion des états d’équilibre. Tout au contraire, par l’établissement des équations de mouvement, nous prenons en considération l’histoire par laquelle de tels états d’équilibre ont pu se produire à partir d’états qui ne sont pas d’équilibre. C’est dire que, dès le départ, la thermocinétique englobe ce que certains ont été obligés d’appeler thermodynamique des états hors d’équilibre.
Le cours d’électrodynamique fait une large part à l’électrostatique et à la magnétostatique. Si les exemples et les applications retenus sont usuels, la présentation des concepts est originale. Le champ primitif introduit par Stueckelberg est le champ de déplacement D⃗(x⃗) (qu’il appelle également champ d’induction électrique) généré par les charges électriques via le théorème de Gauss (appelé également loi de l’induction électrique). Il suppose alors que la densité d’énergie interne locale u(x⃗, D⃗(x⃗)) (au sens de la thermodynamique) est une fonctionnelle du champ d’induction et il définit le champ électrique E⃗(x⃗) comme la variable thermodynamique conjuguée, c’est-à-dire par la dérivée fonctionnelle de u(x⃗, D⃗(x⃗)) par rapport à D⃗(x⃗). Ceci établit d’emblée les natures contravariante de D⃗(x⃗) = {Di(x⃗)} et covariante de E⃗(x⃗) = {Ei(x⃗)}. En électrodynamique linéaire le tenseur diélectrique ∈ki, considéré comme décrivant la structure de l’espace où agissent les champs, permet de « monter » et « d’abaisser » les indices. La force exercée sur un système électrique s’obtient en calculant le travail requis pour déplacer les charges. De ces considérations découlent la loi de Coulomb et l’interprétation du champ électrique comme champ de force sur les charges. Ainsi la loi de Coulomb, souvent adoptée comme point de départ de l’électrostatique, apparaît ici comme une conséquence des définitions.
Dans un premier temps, Stueckelberg tente de développer la magnétostatique en analogie avec l’électrostatique. Il introduit comme champ primitif le champ magnétique H⃗(x⃗) produit par un système de courants stationnaires selon la loi d’Ampère, puis la densité d’énergie magnétique u(x⃗, H⃗(x⃗)), et sa variable thermodynamique conjuguée B⃗(x⃗) (appelée induction magnétique), cependant avec un signe opposé à celui qui intervenait en électrostatique dans la définition de E⃗(x⃗). On regarde ensuite le travail requis par le déplacement d’un système de courants stationnaires d’intensités maintenues constantes dans chaque tube de courant: ce travail est appelé « travail géométrique ». On en déduit alors la loi de force de Biot et Savart, le choix de signe assurant qu’on a bien les bonnes propriétés d’attraction entre deux courants filiformes parallèles si la susceptibilité magnétique µ est positive (ce qui est expérimentalement vrai). Mais Stueckelberg constate que, contrairement au cas électrique, un tel système de courants invariables n’est pas stable : la deuxième variation de u(x⃗,H⃗(x⃗)) par rapport à H⃗(x⃗) est négative!
Pour satisfaire l’existence d’une stabilité thermodynamique il conclut que, lors du déplacement des courants, il faut ajouter au travail géométrique une autre forme de travail d’origine non mécanique appelé travail d’induction, travail nécessaire au maintien des courants.
Il argumente ensuite que, pour obtenir sa forme correcte, l’énergie doit être considérée comme fonctionnelle du champ d’induction B⃗(x⃗) et non du champ magnétique H⃗(x⃗) comme l’aurait indiqué l’analogie électrostatique. Le passage de la variable thermodynamique H⃗(x⃗) à B⃗(x⃗) s’opère par transformée de Legendre, ce qui permet de déterminer la forme du travail d’induction, puis la loi de Faraday. On voit à nouveau le rôle joué par les raisonnements thermodynamiques et l’ordre inversé des arguments, puisqu’habituellement on commence par énoncer la loi de force de Biot et Savart et celle d’induction de Faraday. Une particularité de Stueckelberg consiste à laisser le choix du système d’unité ouvert tout au long du cours. Ceci alourdit l’écriture mais lui permet de discuter le nombre de constantes fondamentales indépendantes intervenant dans la théorie. Une autre rédaction du cours d’électrodynamique, due à L. Berger, C. Piron et J. Rufenart, peut être trouvée sur le site de Constantin Piron : www.phytheomat.ch
La relativité restreinte est introduite de manière traditionnelle à partir de la formulation quadridimensionnelle des équations de Maxwell de l’électrodynamique. La métrique non euclidienne de l’espace-temps est obtenue à partir des relations entre les différents champs électromagnétiques dans le vide. Le groupe de Lorentz des transformations linéaires des coordonnées spatio-temporelles est caractérisé par l’invariance de cette métrique. L’étude du groupe de Lorentz livre les principales implications de la métrique: vitesse de la lumière comme vitesse maximale, contraction des longueurs, ralentissement des horloges, effet Doppler.
Un état d’un système est défini communément par les valeurs des variables du système sur une surface tridimensionnelle à temps constant d’un référentiel donné. Une particularité de Stueckelberg est d’associer des états du système à des surfaces tridimensionnelles spatiales (à normales temporelles) quelconques, en avant-goût de la relativité générale.
Les grandeurs globales du système sont alors obtenues en intégrant des densités locales sur ces surfaces. Les effets de modifications locales infinitésimales de ces surfaces permettent d’établir des relations entre les grandeurs globales et leurs densités.
Le chapitre 2 se termine par l’examen d’un modèle de substance, la matière poudreuse. Cela conduit à la mécanique relativiste du point matériel.
Le chapitre 3 du Livre III (et le chapitre 5 du Livre IV) constitue la partie la plus originale des cours de relativité de Stueckelberg. Ils incluent la thermodynamique dans la théorie de la relativité, ce qui est exceptionnel. Une particularité de la thermodynamique relativiste est que les transferts d’énergie ne peuvent pas être décomposés de manière invariante en travail et échanges de chaleur. Pour formuler malgré cela le deuxième principe de la thermodynamique on introduit l’entropie comme quantité globale associée à une surface temporelle.
Elle est donnée par une intégrale étendue à la surface d’un flux local d’entropie. Le deuxième principe s’exprime par le fait que l’entropie associée à une surface augmente lorsqu’on passe d’une première surface à une deuxième surface postérieure à la première. Ceci implique l’existence d’une source d’entropie locale positive.
La thermodynamique relativiste d’un fluide à une composante est développée en détail. Les variables d’état spécifiant les états du fluide sont des champs définis sur l’espace-temps. Ils sont solutions d’équations d’évolution obtenues à partir du premier et du deuxième principes. Une contrainte assurant la comptabilité de ces équations fait apparaître la température comme un champ scalaire. La positivité de la source d’entropie implique qu’un espace-temps à quatre dimensions possède au plus une dimension privilégiée qui doit être identifiée au temps.
Le Livre IV commence par la construction du changement non linéaire des coordonnées spatio-temporelles décrivant le passage d’un premier référentiel de Lorentz à un second référentiel accéléré par rapport au premier. La métrique du référentiel accéléré n’est pas lorentzienne et les mouvements observés dans ce référentiel sont interprétés comme des mouvements dans un champ gravifique. Ceci établit une relation entre la gravitation et les déviations de la métrique par rapport à la métrique de Lorentz.
Les chapitres 5 et 6 sont consacrés aux outils mathématiques d’analyse tensorielle et de géométrie différentielle nécessaires pour la formulation de la relativité générale et de sa théorie de la gravitation dans le chapitre 7.
Le chapitre 8 présente l’extension à la relativité générale de la thermodynamique de la relativité restreinte exposée dans le chapitre 3 du Livre III. La thermodynamique exige que l’espace-temps ne possède qu’une seule coordonnée temporelle et l’on présente un argument montrant que ceci n’est possible que dans des espaces-temps de dimensions 4 et 2.
On élabore dans le chapitre 9 le formalisme hamiltonien facilitant la résolution des équations différentielles non linéaires qui déterminent la métrique produite par une distribution de matière donnée. Ce formalisme est utilisé dans le chapitre 10 pour déterminer la forme générale d’une métrique statique à symétrie sphérique.
Cela conduit à la métrique de Schwarzschild d’une masse ponctuelle. Le chapitre 11 est consacré aux orbites planétaires et à la déflexion de la lumière par un champ gravifique. La singularité de la métrique de Schwarzschild n’est pas discutée et il n’est pas fait mention de trou noir.
Le cours de thermodynamique statistique (qu’on appellerait aujourd’hui physique statistique) couvre les matières traditionnelles à cette discipline. Le premier chapitre est consacré à la théorie cinétique du gaz monoatomique dans l’espace de phase d’une molécule (espace µ). Il fait une large part à un rappel de mécanique analytique, en préparation à la dérivation usuelle de l’équation de Boltzmann. La cinématique d’une collision est décrite en détail sans toutefois présenter le calcul explicite de la section efficace. Dans les trois dernières sections, Stueckelberg s’attache à faire le lien entre la théorie cinétique et les équations de la thermodynamique phénoménologique qui lui est si chère (Livre I). Il fait ainsi apprécier la cohérence profonde entre l’approche microscopique et l’approche macroscopique.
Le chapitre 2, plus technique, étend les considérations précédentes aux mélanges de gaz. A cette occasion, il introduit les statistiques de Bose-Einstein et de Fermi-Dirac en termes des probabilités d’occupation de cellules dans l’espace µ, sans recours à aucune notion quantique.
Dans le chapitre 3, Stueckelberg expose la théorie des ensembles de Gibbs, où l’espace de phase Γ de N particules remplace l’espace µ d’une seule particule. Il présente à nouveau un assez long développement de mécanique analytique, rendu un peu ardu pour deux raisons. D’une part Stueckelberg tient à admettre les changements de coordonnées les plus générales dans l’espace Γ, d’où l’emploi de la notation tensorielle et la distinction entre densité vectorielle et densité scalaire. D’autre part, sans l’avoir explicitée au départ, il dérive la structure symplectique de l’espace de phase comme conséquence de la validité des équations de mouvement de Hamilton. En fait, ce niveau de généralité n’est pas indispensable pour la compréhension de la suite, et le lecteur peut s’en tenir à un système de coordonnées cartésiennes fixées une fois pour toutes. L’exposé des principes de la physique statistique proprement dite débute par une définition très générale de l’entropie comme fonctionnelle de la densité de probabilité sur l’espace de phase (section 3.5). L’exigence d’extensivité fixe la forme de cette fonctionnelle, et la formule historique de Boltzmann se déduit comme cas particulier. On retrouve ici le souci de Stueckelberg de partir des prémisses les plus générales possibles.
On constate que l’entropie ainsi définie (dite microscopique) reste constante au cours du temps, si bien que Stueckelberg est conduit à introduire une deuxième entropie (dite macroscopique) par le processus de coarse-graining sur des cellules de l’espace de phase de tailles déterminée par la constante de Planck. L’argument est qu’en vertu du principe d’incertitude le point représentatif ne peut être localisé avec une précision supérieure à l’extension de telles cellules. Cette entropie macroscopique est alors croissante comme le veut la thermodynamique (affirmation donnée ici sans démonstration, section 3.6). Toutefois Stueckelberg ne commente pas plus loin le problème de la compatibilité entre la réversibilité temporelle des équations du mouvement et l’irréversibilité macroscopique. La suite de l’exposé suit les méthodes standards (ensemble microcanonique. canonique, grand canonique et applications) et le cours se termine sur des éléments de physique statistique quantique (chapitre 4).
Dans le chapitre 5 du Livre VI, « Notions et notations de la théorie des quantas », l’originalité du point de vue de Stueckelberg est de placer les états du système physique dans un espace de Hilbert réel, ce qui a quelques avantages. Pour y arriver il part d’observables réelles, avec des mesures probabilistes. Suit une étude poussée du principe d’incertitude de Heisenberg sur les mesures permises qui aboutit à la nécessité d’introduire une matrice J antisymétrique de carré négatif (J2 = –1) . Il montre ensuite l’équivalence de la mécanique quantique sur un espace de Hilbert réel et celle sur un espace de Hilbert complexe.
Pour le chapitre 8, « Théorie du champ scalaire », il faut préciser que champ scalaire quantifié, qui obéit à une équation de Klein-Gordon, était utile à l’époque de Stueckelberg lorsqu’on voulait faire une théorie des interactions nucléaires, médiées par l’échange de mésons π à spin zéro.
Aujourd’hui on travaille avec des quarks (spin ½) dans le cadre de la chromodynamique quantique. Néanmoins, le champ scalaire étant le plus simple, il est utile, du point de vue pédagogique, de commencer par lui et d’apprendre quelles sont les propriétés communes à tous les champs. Cela est d’autant plus vrai si la particule qui correspond au champ (complexe) possède une charge électrique (π±). La conjugaison de charge discutée par Stueckelberg est une opération importante dans la physique des particules. La conservation du courant électrique est un modèle pour toutes sortes de courants qui figurent dans le « Modèle Standard ». Pour la quantification, Stueckelberg essaye des commutateurs et des anticommutateurs. Le deuxième choix aboutit à une contradiction. C’est l’argument de Pauli pour affirmer que les particules de spin zéro décrits par le champ scalaire quantifié obéissent à la statistique de Bose-Einstein.
Au chapitre 9, « Le champ spinoriel quantifié » (spin ½), Stueckelberg étudie d’abord de manière intensive les propriétés algébriques des spineurs et leur interprétation dans la théorie des groupes, notamment du groupe de Poincaré. Les particules de spin ½, électrons, nucléons, quarks, obéissent à l’équation de Dirac. Stueckelberg n’utilise pas les notations habituelles, ce qui peut causer des confusions. Il décrit l’opérateur de charge, les courants conservés, et la conjugaison de charges. Il est important de noter que l’équation de Dirac est relativiste. Stueckelberg envisage de nouveau deux possibilités de quantification. Mais les électrons obéissent au principe d’exclusion de Pauli, ce qui implique la quantification par des anticommutateurs et la statistique de Fermi-Dirac.